Вычисление полинома от нескольких переменных |
|
В самом общем виде степенной полином от нескольких переменных можно записать формулой То есть в полином входят все одночлены, в которых сумма степеней переменных не превышает порядка полинома Вычислять каждый одночлен по-отдельности — не лучшая идея. Если верить известной книге Numerical Recipes, то когда машины захватят мир, люди, виновные в подобном издевательстве над компьютером, будут немедленно казнены. На самом деле каждый одночлен порядка k может быть вычислен по одному из одночленов порядка k-1 с помощью только одного умножения. Например, одночлены первого порядка множим на одну из переменных и получаем одночлены k-го порядка. Однако, начиная со второго порядка появляется проблема: одночлен При таком подходе каждый одночлен служит для вычисления сразу нескольких других. Степени  Рис. 1. Процесс вычисления одночленов многомерного полинома, представленный в виде дерева. Каждый узел соответствует одночлену, а каждое ребро — домножению на одну из переменных. Вычислительный процесс представимый в виде дерева наиболее естественно реализуется с помощью рекурсивного алгоритма. В наиболее простом варианте рекурсивная процедура вычисляет один одночлен и вызывает себя для вычисления всех дочерних одночленов. Такая процедура представлена ниже:
//***********************************************************
//* Процедура для рекурсивного вычисления массива одночленов.
//* Один вызов процедуры - подсчет одного одночлена.
//***********************************************************/
procedure OneMonomial(
//Ссылка на вещественнозначный массив, куда записываются
//вычисленные одночлены.
var Monomials: array of extended;
//Номер предыдущего одночлена (по которому будет производится
// вычисление текущего).
Parent: integer;
//Ссылка на массив значений переменных
var x: array of extended;
//Количество переменных
D: integer;
//Номер переменной, на которую надо домножить родительский одночлен
xnum: integer;
//Количество уже вычисленных одночленов
//(чтобы знать куда записывать новый).
var MN: integer;
//Порядок одночлена, он же глубина рекурсии
Order: integer;
//Порядок полинома, он же максимальная глубина рекурсии
n: integer;
);
var
i: integer;
begin
MN := MN + 1;
Monomials[MN] := Monomials[Parent] * x[xnum];
if Order < n then
begin
Parent := MN; //Запоминаем значение текущего
for i := xnum to D-1 do
OneMonomial(Monomials, Parent, x, D, i, MN, Order + 1, n);
end;
end;
Общее количество одночленов в полиноме порядка n от D переменных можно рассчитать по формуле Вычисление массива одночленов с помощью приведенной выше процедуры выглядит так:
SetLength(Monomials, Number);
Monomials[0] := 1;
MN := 0;
if n > 0 then
for i := 0 to D-1 do
OneMonomial(Monomials, 0, x, D, i, MN, 1, n);
Если вычисления требуется проводить много раз для разных значений x, то для ускорения работы следует избавится от рекурсии. Простой способ это сделать состоит в том, чтобы сделать рекурсивный обход дерева один раз и при этом для каждого одночлена запомнить номер родительского одночлена и номер переменной, на которую он множился. Затем эту информацию можно использовать для вычисления одночленов без рекурсии. Соответствующий код выглядит так:
//Создадим ту же процедуру OneMonomial, но вместо вычисления
//одночлена будем лишь запоминать параметры Parent и xnum
procedure OneMonomial(
Parent: integer;
D: integer;
xnum: integer;
var MN: integer;
Order: integer;
n: integer;
//Ссылка на массив для запоминания номеров родительских одночленов
Parents: array of ineger;
//Ссылка на массив для запоминания номеров переменных
VarNumbers: array of integer;
);
var
i: integer;
begin
MN := MN + 1;
//Вычислений теперь не делаем
//Monomials[MN] := Monomials[Parent] * x[xnum];
//Вместо этого:
Parents[MN] := Parent;
VarNumbers[MN] := xnum;
if Order < n then
begin
Parent := MN; //Запоминаем значение текущего
for i := xnum to D-1 do
OneMonomial(Parent, D, i, MN, Order + 1, n, Parents, VarNumbers);
end;
end;
Вызов этой процедуры производим так:
SetLength(Parents, Number);
SetLength(VarNumbers, Number);
MN := 0;
if n > 0 then
for i := 0 to D-1 do
OneMonomial(0, D, i, MN, 1, n, Parents, VarNumbers);
А вычисление массива одночленов для каждого значения переменных x так: SetLength(Monomials, Number); Monomials[0] := 1; for i := 1 to Number-1 do Monomials[i] := Monomials[Parents[i]] * x[VarNumbers[i]]; Практика показывает, что такое нерекурсивное вычисление производится заметно быстрее рекурсивного. Вернемся теперь к вычислению собственно полинома. Такое вычисление будет получатся обходом узлов дерева одночленов с умножением их на соответствующие коэффициенты и суммированием. Это приводит нас к следующей формуле: Здесь индексы Данная формула является обобщением на многомерный случай хорошо известной схемы Горнера для вычисления одномерного полинома: Функция, производящая вычисления в соответствии с формулой (4), представлена ниже:
function Horner(
//Коэффициенты, упорядоченные также как одночлены,
//вычисляемые приведенной выше процедурой.
var c: array of extended;
//Аргументы полинома
var x: array of extended;
//Размерность полинома (количество аргументов)
D: integer;
//Порядок полинома
n: integer;
//Номер очередного одночлена
var MN: integer;
//Глубина рекурсии (она же - порядок очередного одночлена)
depth: integer;
//Номер переменной, начиная с которого производится домножение.
//В зависимости от глубины рекурсии соответствует i_1, ..., i_n
//в формуле (4).
i_depth: integer;
);
var
i: integer;
P: extended;
begin
P := c[MN]
MN := MN + 1;
if depth < n then
for i := i_depth to D-1 do
P := P + x[i] * Horner(c, x, D, n, MN, depth+1, i);
Horner := P;
end;
Чтобы скрыть служебные в общем-то параметры MN, depth, i_depth следует вызывать эту функцию через другую:
function Polynomial(
//Коэффициенты
var c: array of extended;
//Аргументы полинома
var x: array of extended;
//Размерность полинома (количество аргументов)
D: integer;
//Порядок полинома
n: integer;
);
var
MN: integer;
begin
MN := 0;
Polynomial := Horner(c, x, D, n, MN, 0, 0);
end;
|
Персональная страничка
| ||
|
|

Могу прислать процедуры для Питона и Фортрана, которые вычисляют индекс родительской функции и индекс множителя. Если хочешь, повесишь их у себя на сайте.
Кстати, неплохо было бы организовать подсветку синтаксиса. Может быть, есть какой-нибудь плагин для распространённых языков, а то руками и правда подсвечивать загребёшся.
Присылай.
Подсветка будет. Я пользуюсь SyntaxHighlighter‘м. Там нет фортрана, но найду и для него скрипт. Будет код, будет и подсветка.
Код прислал.
хорошая статья, очень даже помогли. хотелось бы конечно увидеть рассуждения о сложности вычисления…
>>рассуждения о сложности вычисления
Вычисление каждого одночлена требует одного умножения. Всего одночленов
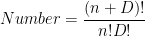
штук.
спасибо! не ожидал, оперативно работаете)
Схема Горнера является расходящейся. Хотя сам вычисляю по ней.Ваше представление о многомерных полиномах неполно. Еще в 1992 году Я уже все разработал. Сейчас вернулся и кое что добавил. Кол-во неизвестных равно не (n+d)!/n!/d!. а можно свести к N*d
Поделитесь ссылкой, если не трудно.
Ребят помогите пождалуитс, ооочень срочно нужна задача на C++ Наити Значение многочлена по схеме Горнера
матричная теория полиномов
Схема Горнера устарела
3fdeb5